I am currently working in biomedical engineering, and it is fairly common to have to use the distance transform. The distance transform (DT) is very CPU intensive and very easily parallelizable, so I decided to take at shot at implementing it on GPU (since it is the trendy thing to do these days).
The OpenCL file for the DT in itself is very simple:
//File: clDistanceTransform.cl
__kernel void DistanceTransform(
__global const float* vIn,
__global float* vOut,
int iDx,
int iDy)
{
int iGID = get_global_id(0);
if (iGID >= (iDx*iDy))
{
return;
}
float minVal = MAXFLOAT;
int minX = 0;
int minY = 0;
for(int y = 0; y < iDy; y++)
{
for(int x = 0; x < iDx; x++)
{
if(vIn[y*iDy + x] >= 1.0f)
{
int idX = iGID % iDy;
int idY = iGID / iDy;
float dist = sqrt( (float)((idX-x)*(idX-x) + (idY-y)*(idY-y)) );
if(dist < minVal)
{
minVal = dist;
}
}
}
}
vOut[iGID] = minVal;
}
The C++ version used for comparison is also fairly simple:
/**
* @brief Compute distance transform
* @note Assumes that imOutput is of the proper size
*/
template <class T>
void cppComputeDistanceTransformImage(const Image<T>& imInput, Image<T>& imOutput)
{
static const float thresholdVal = 1.0f;
assert( imInput.getTotalSize() == imOutput.getTotalSize() );
const size_t dx = imInput.getDx();
const size_t dy = imInput.getDy();
const float* dataPtrInput = imInput.getDataPtr();
float* dataPtrOutput = imOutput.getDataPtr();
//Outer loop (for every posistion in output image)
for(size_t x=0; x < dx; ++x)
{
for(size_t y=0; y < dy; ++y)
{
//Inner loop (... get the closet position above threshold in input image)
T minDist = std::numeric_limits<T>::max();
for(size_t ox=0; ox < dx; ++ox)
{
for(size_t oy=0; oy < dy; ++oy)
{
if( dataPtrInput[dy*oy + ox] >= thresholdVal )
{
float dist = std::sqrt(
static_cast<float>((ox-x)*(ox-x)) +
static_cast<float>((oy-y)*(oy-y)) );
if( dist < minDist )
{
minDist = dist;
}
}
}
}
dataPtrOutput[dy*y + x] = minDist;
}
}
}
There is a fair amount of code in order to compare it with the CPU 'vanilla' implementation (as well as a module to automatically create Matlab tables in order to graph the results) -- see the 'download' section.
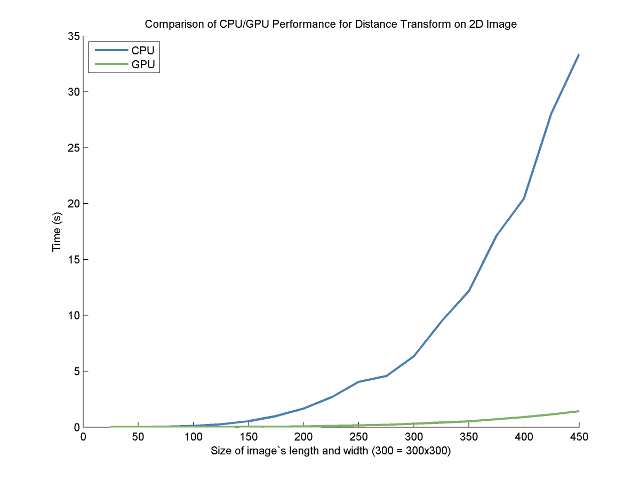
Here are the raw results:
Test the speed of DT on CPU
CPU:
Size: 25, run time: 0.000463337s
Size: 50, run time: 0.00692592s
Size: 75, run time: 0.0344292s
Size: 100, run time: 0.105547s
Size: 125, run time: 0.257267s
Size: 150, run time: 0.532334s
Size: 175, run time: 0.983563s
Size: 200, run time: 1.66177s
Size: 225, run time: 2.66493s
Size: 250, run time: 4.06146s
Size: 275, run time: 4.5738s
Size: 300, run time: 6.34406s
Size: 325, run time: 9.45664s
Size: 350, run time: 12.1828s
Size: 375, run time: 17.1442s
Size: 400, run time: 20.4721s
Size: 425, run time: 28.1132s
Size: 450, run time: 33.3803s
Test the speed of DT on GPU
GPU:
Size: 25, run time: 0.00330699s
Size: 50, run time: 0.00153775s
Size: 75, run time: 0.0038303s
Size: 100, run time: 0.00666152s
Size: 125, run time: 0.011251s
Size: 150, run time: 0.0301451s
Size: 175, run time: 0.0407184s
Size: 200, run time: 0.0582057s
Size: 225, run time: 0.104097s
Size: 250, run time: 0.160872s
Size: 275, run time: 0.208102s
Size: 300, run time: 0.308096s
Size: 325, run time: 0.411383s
Size: 350, run time: 0.524591s
Size: 375, run time: 0.704087s
Size: 400, run time: 0.897559s
Size: 425, run time: 1.13865s
Size: 450, run time: 1.42005s
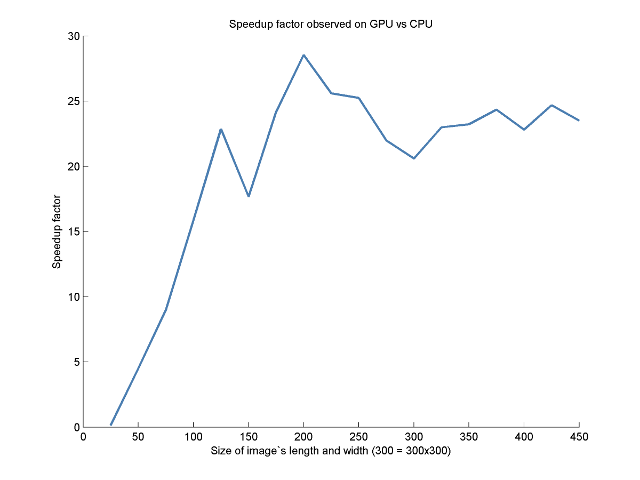
On a fairly standard NVIDIA card (GeForce GTX 260), the speedup factor is about 25.

It is interesting to see that using the CPU one can use bigger images in real-time with a much smaller impact on performances:
I guess that there are ways to implement on GPU that would lead to a better speedup. But when there is a need for speed and a distance transform, propagation methods that are inherently faster are used instead of a distance transform (ex: GPU-Based Euclidean Distance Transforms and Their Application to Volume Rendering by Jens Schneider). They then go on to implement those method on GPU and get fantastically fast results.
You can download the full source code and (windows) binaries: GPUDistT.zip